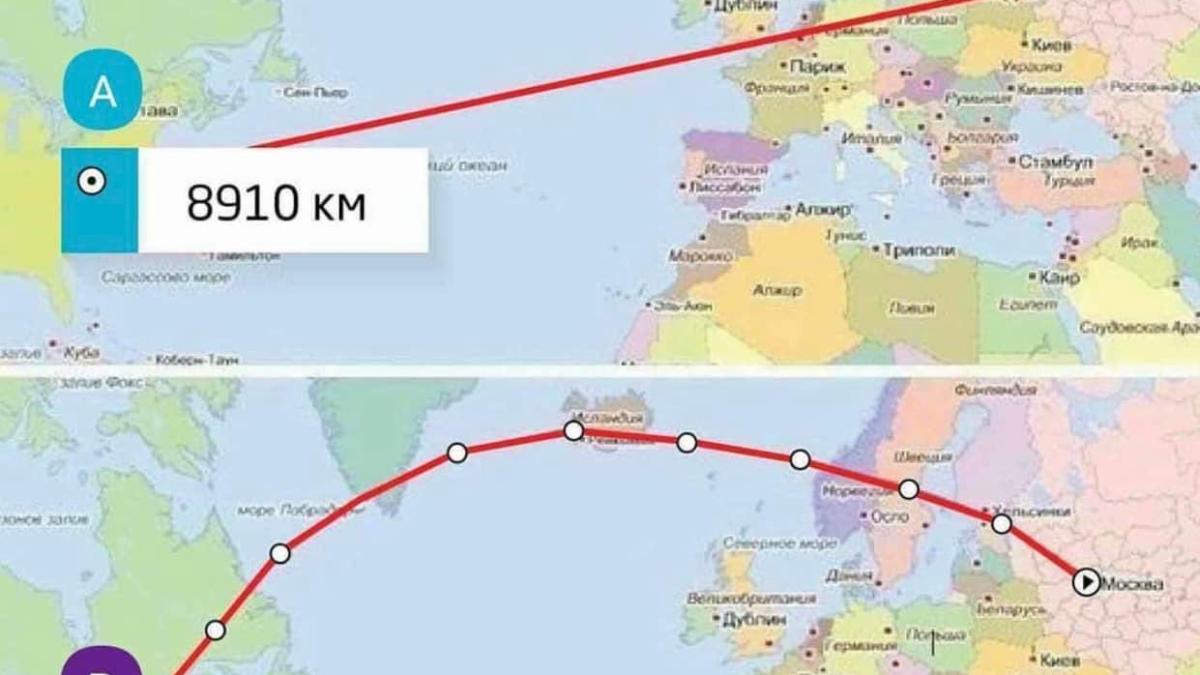
De ce traseul curbat al unui avion e mai scurt decât cel în linie dreaptă, până la destinație

Ruta cea mai scurtă între două puncte pe suprafața Pământului este de-a lungul unui astfel de cerc mare.

Spre exemplu gândește-te la o bandă elastică întinsă pe un glob între două puncte. Aceasta urmează curba unui cerc mare, nu o linie dreaptă. De exemplu, ruta dintre New York și Tokyo urmează un arc de cerc care trece peste Alaska, nu o linie dreaptă de pe o hartă.

Cele mai comune hărți (precum proiecția Mercator) sunt reprezentări plane ale unui Pământ sferic. Din cauza acestei distorsiuni, rutele reale, care sunt mai scurte pe glob, apar ca fiind curbe pe hartă.

O linie dreaptă trasată pe o hartă de la Londra la Los Angeles poate părea logică, dar pe un glob real, ruta ar trece mai aproape de Groenlanda dacă vrem să fie cea mai scurtă.

Pe o sferă, distanța cea mai scurtă între două puncte este un arc de cerc mare, nu o linie dreaptă proiecționată pe o hartă plană. Calculul distanței implică formule geometrice specifice sferei, nu planei.

De e exemplu dacă călătorești între două orașe pe același meridian (nord-sud), traseul cel mai scurt este de-a lungul meridianului (care face parte dintr-un cerc mare). O linie dreaptă, pe o hartă plană, ar părea să meargă „în afara” sferei

Dacă desenăm o linie între două puncte de pe o portocală (care reprezintă globul Pământului), cea mai scurtă rută este cea care urmează suprafața curbată a portocalei, nu o linie dreaptă care ar tăia prin interiorul fructului.

Așadar ruta curbată (care urmează un cerc mare) este mai scurtă decât linia dreaptă de pe o hartă plată deoarece ține cont de geometria sferică a Pământului. Aceasta este regula fundamentală a navigației pe o planetă rotundă.

  Fiți la curent cu ultimele noutăți. Urmăriți DCNews și pe Google News