€ 5.0920 →
|
$ 4.3235 →
|
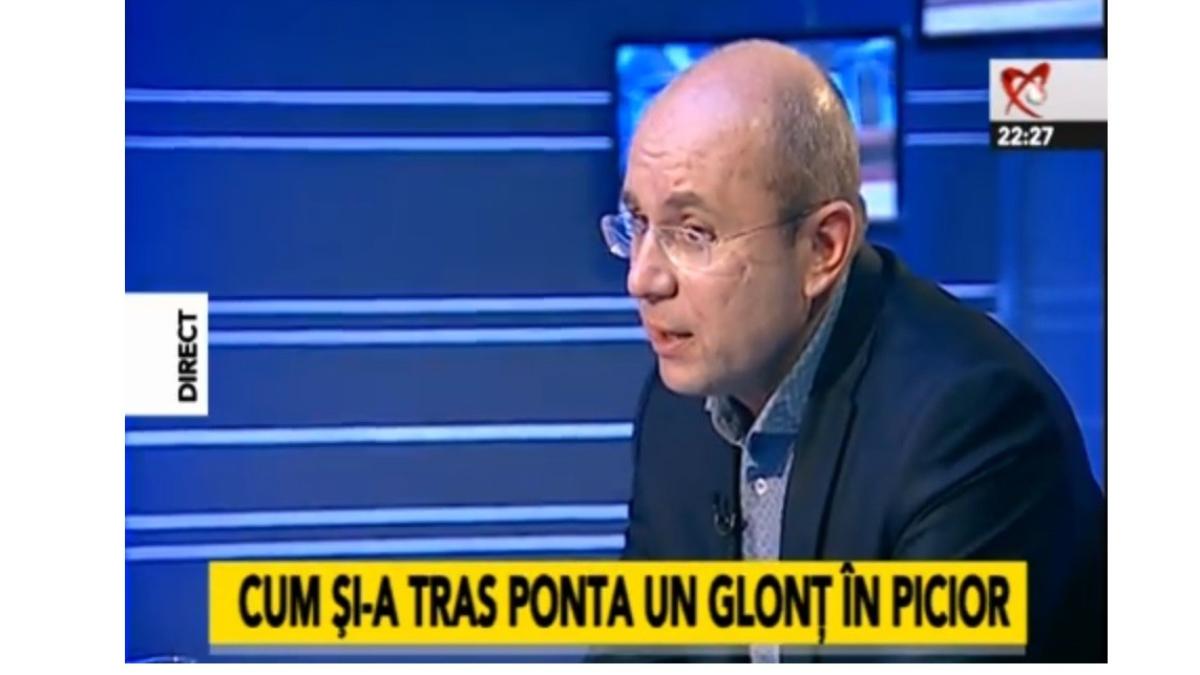 Captură Realitatea
Captură Realitatea
Cozmin Gușă a fost, marți seara, invitatul lui Rareș Bogdan la emisiunea „Jocuri de Putere” de la Realitatea.
„PSD se află în cea mai grea situație a sa de după 1989. Mult mai grea decât în 2005. În 2005, PSD-ul era ranforsat de către niște lideri de forță, un Adrian Năstase, care nu a plecat de tot, a rămas președinte executiv, sigur, în coasta lui Mircea Geoană, care câștigase în fața lui Ion Iliescu, ceea ce nu a fost ușor. Dimpotrivă. Și cu legitimitatea unei înfrângeri la limită. Chiar și în 2009, PSD-ul mai avea o legitimitate pentru că PSD-ul câștigase alegerile în România. El fusese învins de Baconschi și ai lui, prin contribuția negativă a lui Titus Corlățean care a avut grijă de diaspora. Lumea a uitat aceste lucruri”, este de părere Gușă.
„Astăzi, Victor Ponta este în fața unei înfrângeri pe care nu a suferit-o în fața unui Băsescu, cu sceptrul puterii în mână, cum a fost Mircea Geoană, în 2009. A pățit-o în fața unui domn care nu a făcut politică, dublu minoritar, lucru care a fost considerat un handicap. Uite că nu este, că românii s-au normalizat. Și a suferit-o la aproape 9 puncte procentuale, ceea ce este un megadezastru pentru partid, cu marea majoritatea a mediei de partea sa, și cu toți banii în buzunar, de prim-ministru. Este o chestie care va fi analizată în toate manualele de marketing politic. Cât de prost poți să fii să pierzi toate aceste oportunități? Asta va fi studiu de caz la Facultatea de Științe Politice de la Oxford!”, a declarat Cozmin Gușă la Realitatea.
Fiți la curent cu ultimele noutăți. Urmăriți DCNews și pe Google News